1 前言
先前一直想就Optistruct结构优化方面写个专题,但一直没有找到以怎样一种形式开始比较好。如果从优化相关的理论说起,一方面个人水平没到,另一方面会导致很多没有接触过的伙伴压根看不懂;但是直接从软件的一些控制参数开始讲起又显得些许无趣。因此决定以这种案例的形式来进行说明,每个案例都会有自己的重点,希望读者能仔细体会。
2 案例说明
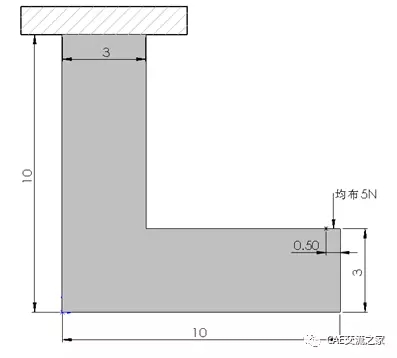
图 1模型示意图
如图所示L型结构(厚度0.1mm),其上端固支于壁面,右端作用一向下的大小为0.05N的荷载,作用范围为0.5mm。现欲对结构减重70%以上且拐角处应力不超过400MPa。
材料属性:弹性模量210000MPa,泊松比0.3
3 问题分析
该问题显然是个优化问题,第一个要求:减重70%说明需要对结构开孔,将应力远远低于许用应力的部分去掉,这属于拓扑优化范畴。第二个要求:拐角处应力不超过400MPa说明需要优化拐角处的形状,避免应力集中,这属于形状优化范畴。
至于如何去理解本例的拓扑优化和形状优化,这里我以两者描述问题的不同来简单区分。
拓扑优化描述的是如何排布单元使得整体结构的性能指标达到最优,实际是描述设计空间中单元的有无问题(哪里需要单元,哪里不需要)。它本身只是在给定的设计空间中不断删除或者添加单元,但是本身并不会超出给定的设计空间,比如本例进行拓扑,最终构型不会超出L型。
形状优化从直观上去理解就是优化结构的外形,实现的方式是将节点位置作为基本设计变量,这样通过节点位置的改变来实现形状的改变,从而来或得满足设计要求的形状。它本身不会自主的去删除单元,而仅仅是将作为设计变量的节点的位置进行改变,可以直观理解为一种节点拖拽。
4 Optistruct实现流程
由于重点是优化,所以本文直接省略前处理部分,直接从优化开始。这里需要说明的是,这里虽说是案例但是是以交流为角度展开的,并不是教程。下面是前处理完成后的模型(使用板壳单元进行建模):

图 2有限元分析模型
4.1 初次分析
初次分析的目的是为了确定初始结构的性能,比如刚度,强度等。本例初次分析的重点是获悉在该网格尺寸下结构的应力分布以及拐角处的应力水平(虽然理论上拐角处应力无限大的,但是在该网格尺寸下仍然可以作为设计目标。)
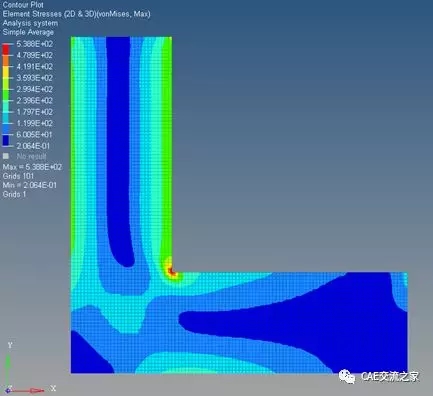
图 3 Mise应力云图(Simple方式平均)
如上图所示,该结构的应力分布已经比较清晰的展现在了我们的面前,这可以有助于我们对拓扑的结果进行一个合理的判断。通过观察应力云图,我们可以获悉L型上面部分两侧绝对是主传力路径的一部分,深蓝色区域是整个结构中的“闲置”部分,拐角处集中应力达到了538MPa。
4.2 减重
对结构应力分布情况有了基本了解之后,我们开始进行减重的优化设计。对于一个基本的优化问题,我们至少有三要素:目标函数,设计变量以及约束条件。
通过最开始的问题分析,我们知道该问题的目标函数为整体的刚度,设计变量为单元的密度(密度体现了单元的有无问题),约束条件为重量<30%原结构。
对应于软件,我们只需要告诉它这三个要素即可,所有的设置都在analysis(分析)>optimization(优化)面板中进行。

图 4 topology面板
通过上图topology(拓扑),我们定义了设计变量(也即设计空间)为所有单元。
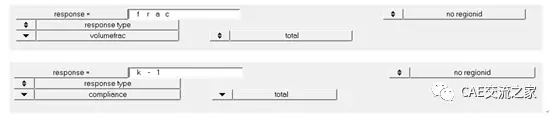
图 5 response面板
通过上图response(响应),我们定义了两个响应,这两个响应一个(体积比)用于定义约束条件,另一个(整体柔度)用于定义目标函数。

图 6 constrain面板
上图constrain(约束)定义了一个约束条件,即体积比上限为0.3,这意味着最后优化结果最多占总体结构体积的30%(均匀密度材料的质量问题转化为体积问题)

图 7 objective面板
上图objective(目标)定义目标为总体柔度最小(即刚度最大)。
下面重点来了,按照上述参数我们并不能得到想要的结果,它或许是最优的,但并不一定是方便设计或者可用于设计的。一般对于一个优化问题,我们需要根据实际情况添加一些额外约束,这里称之为制造约束(主要是考虑到制造方面难易的一些因素)。

图 8最小尺寸控制
一般情况下我们会添加mindim(最小尺寸控制),这是为了防止出现局部细小的支架结构,因为这些结构往往很难或者无法制备。这里我添加最小尺寸约束为1mm,也即优化的结果中主传力路径至少为1mm(这并不是一个强约束,意味着结果中还是有很多大于1mm的部分,后面会进行讨论)。
除了工艺约束外,我们有时候还需要调整算法方面的一些参数,就像我们做非线性分析需要调整时间步长,接触刚度等一样,对于一个优化问题也有些参数针对具体问题需要调整。

图 9离散度(罚系数)控制
上图我设置了离散度为2,这个离散度在基于SIMP的拓扑优化问题中是一个核心概念,就像最开始的问题分析中,将拓扑优化描述成单元有无的问题,也就是存在还是不存在的问题。可以感受到,这是一个典型的离散问题,只能选择存在或者不存在,要么0(不存在),1(存在)。但是计算机更擅长处理一个连续的问题,因此我们将0、1问题变成0~1问题,但是为了防止问题本质的改变,我们必须构造一种方法,使得在连续问题下,单元也会向着0、1演变,而不容易停留在类似于0.5这种中间数值(中间密度会造成难以识别的优化边界)。如何去构造就引出了下面的核心式子:
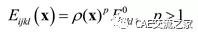
这个式子中的上标P就是我们的离散度,E为弹性模量,ρ为密度。当P越大我们可以感受到密度与弹性模量之间的关系的非线性程度越大,这种非线性有什么用?我们可以通过下面这个图来解释
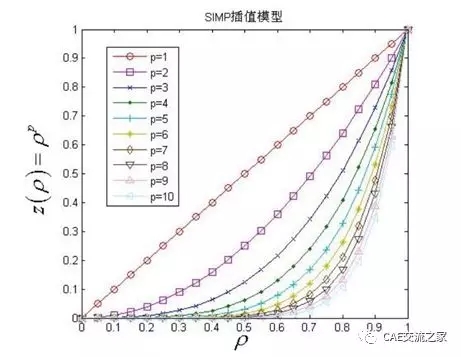
图 10 SIMP插值模型
当P=1,我们可以看到密度和弹性模量呈线性关系,当P=2,两者是平方关系,这种关系导致了单元在密度(代表了质量)和弹性模量(代表了刚度)之间需要进行权衡,比如在密度=0.8时,密度增加0.1,可能会导致弹性模量增加0.2倍(假设),这就意味着算法认为一直增加密度会导致刚度增加更多,因此最终会跑到密度=1;反之如果密度=0.2,增加0.1密度,弹性模量可能只增加0.05倍(假设),那么算法认为我继续增加密度不利于找到最优解,因此向着密度=0跑去。因此,当离散度(罚系数)增大,优化的结果越接近于原始的0、1问题。这个系数取为2(平面问题)、3(空间问题)是推荐值,过大的话理论上可行但是结果往往没有推荐参数好(理解下,这里的好不是指数学上的好,而是工程上的),这里暂时不做探讨,使用推荐值2。
设置好上述参数后我们进行优化计算,得到如下结果:
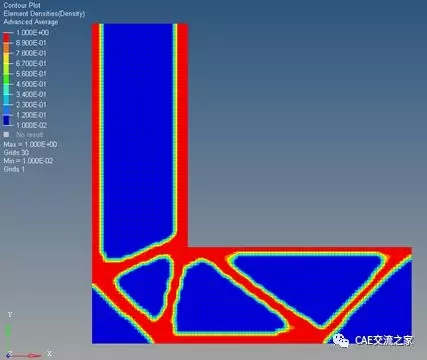
图 11拓扑优化结果
如果我们隐去密度小于0.3的部分将会得到完整的结构外形,这个构型的刚度理论上是在该网格密度下“最优”的(由于拓扑优化依赖于网格尺寸,因此这里必须强调在该种网格尺寸下的“最优”解)。
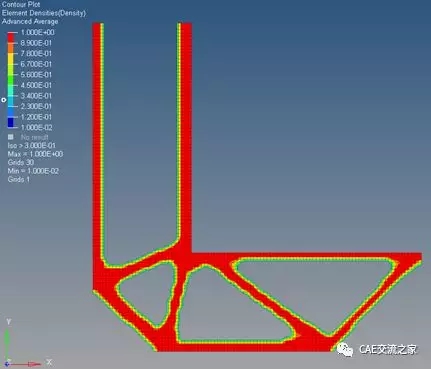
图 12拓扑优化结果(隐去密度小于0.3)
将该结果导出为stl格式,然后倒入任意三维建模软件进行重新建模。本例由于是二维模型,因此建模软件不受限制,但如果是三维模型,建议导入SolidThinking Evolve中进行二次建模。这里模型比较简单使用Solidworks进行建模即可,结果如下:

图 13二次几何模型
4.3 对拓扑结果的分析
这一部分是本文的核心,很多文章都会写到如何使用Optistruct进行拓扑优化,但是可能会回避里面的一些问题,这里我准备就这些问题好好和大家交流下(如何理解这些问题是做出一个好的优化设计的前提,不光是拓扑优化)。但是本文中我暂时不发表言论,算是留给大家一部分思考空间,欢迎下方留言讨论。
4.3.1 应力水平
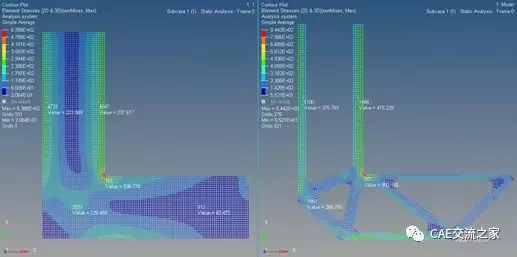
图 14优化前后应力水平比较
观察整体结构各部位的应力水平,可以看到几个问题:
原始结构主要承力部分Mise应力为230MPa,闲置部分Mise应力为50MPa;优化后结构主要承力部分Mise应力415Mpa,闲置部分170MPa。这个体现了轻量化设计的一个核心:将分担给闲置(应力水平较小)部分的承载施加到主传力路径,相当于“能者多劳”。但是在这种模式下,结构应力达到415MPa(假设400MPa为屈服极限),这时候我们该怎么办?
拓扑作为一个优化问题,我们想要找到最优解,但是软件给的结果真的是最优的吗,还是只是较优?(考虑下优化后仍有一定的“闲置”部分)
很多做分析的伙伴看到那个拐角肯定会很不舒服,那的确是个不合理的结构。但是对于该问题,如何找到拐角处的合理结构?在该例中再加上应力约束是否是一种较好的方法?(分析一个复杂问题的时候我们往往会留主和分解,考虑下优化)
4.3.2 刚度情况
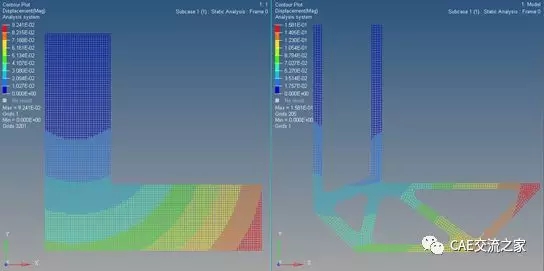
图 15优化前后刚度比较
刚度情况我们可以通过结构的最大位移简单比较,可以看到原始结构最大位移0.0924mm,优化后结构0.158mm。于是就有人问了,我优化这个结构的刚度,为什么整体刚度反而降低了?这是一个简单但是很重要的问题,体现了我们何时知道需要优化以及怎么去优化。
4.3.3 工艺约束
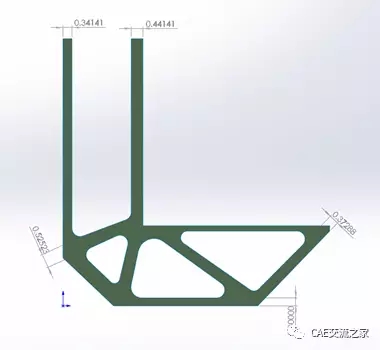
图 16二次几何模型主体尺寸
还记得分析中我们加了制造约束—最小尺寸1mm吗?但是我们仔细看看优化后的结果,0.34mm,0.44mm,0.52mm,0.3mm,这些主要的边界貌似都比1mm小。怎么回事?是软件傻还是我们傻?
4.3.4 网络依赖性
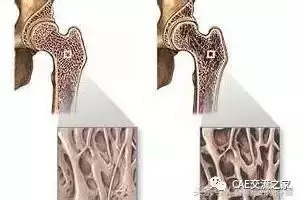
图 17骨头微结构
文中强调过:该种网格下的“最优”解。其中“最优”这个已经在第一问中提出了,那么怎么去理解这个“该种”网格。如果网格不断细化,结果会变成什么样?(想象下人的骨头中错综复杂的微结构或者树叶的脉络)

